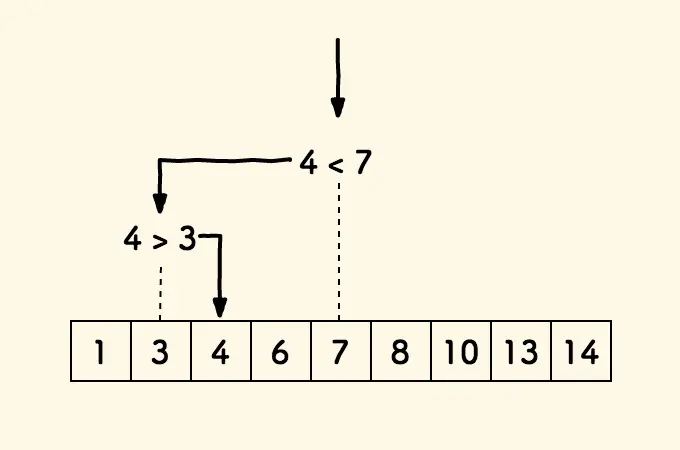
LogTrick 方法解决子数组最值或计数问题
Logtrick 是在时间复杂度为 计算子数组问题的基础上,利用 |,&,lcm,gcd 等性质优化的一种算法。 通常用于求 子数组 经过一些操作 (gcd,lcm,&,|) 后的 max、 min 或者计数问题。
本文将分为两大部分讲解 LogTrick 的理解:
- 子数组经过一些操作后的最值问题
- 子数组经过一些操作后的计数问题
本文题目难度标识:🟩简单,🟨中等,🟥困难。
最值问题
OR 运算 - 最值问题
给你一个数组 nums 和一个整数 k 。你需要找到 nums 的一个子数组,满足子数组中所有元素按位或运算 OR 的值与 k 的 绝对差 尽可能 小 。换言之,你需要选择一个子数组 nums[l..r] 满足 |k - (nums[l] OR nums[l + 1] ... OR nums[r])| 最小。
请你返回 最小 的绝对差值。
子数组 是数组中连续的 非空 元素序列。
限制:
1 <= nums.length <= 10^51 <= nums[i] <= 10^91 <= k <= 10^9
从暴力方法开始讲起
我们可以想到一个 的暴力算法:
1 | // 暴力算法,会超时 |
方法的要点在于把子数组相或的结果存储在 nums 中。

复杂度分析:
- 时间复杂度:
- 空间复杂度:。
Trick!
为了充分利用 OR 的性质,我们还可以对内层循环进行优化。
内层循环 j 在递减时,如果 x 和当前 nums[j] 相或不再发生变化,那么和 nums[j-1]、nums[j-2] … nums[0] 相或也不会发生变化。这时我们可以跳出循环了。

1 | class Solution { |
当 j 在递减时,x 能让当前 nums[j] 的一些比特位从 0 变为 1,如果不能就会退出内层循环。x 最大值限制为 10^9,即 x 最多有 29 个比特位,也就是说,x 最多能进行 29 次内部循环(第二重循环)。因此在本题中,内部循环的时间复杂度将是一个常数。
复杂度分析:
- 时间复杂度:,其中 n 是 nums 的长度,。
- 空间复杂度:。
这种方法之所以被称为 LogTrick ,是因为它巧妙地利用了 OR 运算的性质,并且其时间复杂度与数字的位数(logarithm of the number)相关。
相关题目:
- 🟨 3097. 或值至少为 K 的最短子数组 II - 力扣(LeetCode)
- 🟨 2411. 按位或最大的最小子数组长度 - 力扣(LeetCode) 需要维护答案数组
- 🟨 898. 子数组按位或操作 - 力扣(LeetCode) 变种题。某种程度上可以理解为最值问题。
AND 运算最值问题

Winston 构造了一个如上所示的函数 func 。他有一个整数数组 arr 和一个整数 target ,他想找到让 |func(arr, l, r) - target| 最小的 l 和 r 。
请你返回 |func(arr, l, r) - target| 的最小值。
请注意, func 的输入参数 l 和 r 需要满足 0 <= l, r < arr.length 。
参考答案:
1 | class Solution { |
内层循环 j 在递减时,如果 x 和当前 nums[j] 相与不再发生变化,说明 x 不足以让当前位置 nums[j] 变小,即 x 以及不能去掉 nums[j] 表示的集合中的比特位 1。而 nums[j-1]、nums[j-2] … nums[0] 都和 nums[j] 相与过,能被去掉的比特位 1 早就被 nums[j] 所表示的集合去掉了,因此 x 与 nums[j-1]、nums[j-2] … nums[0] 进行与运算也不会发生变化。
复杂度分析:
- 时间复杂度:,其中
n是arr的长度,。由于 ,二进制数对应集合的大小不会超过 29,因此在 AND 运算下,每个数字至多可以减少 29 次。总体上看,二重循环的总循环次数等于每个数字可以减少的次数之和,即 。 - 空间复杂度:。
计数问题
AND 运算的计数问题
给你一个整数数组 nums 和一个整数 k ,请你返回 nums 中有多少个 子数组 满足:子数组中所有元素按位 AND 的结果为 k 。
List + 原地去重法
在上一节的 OR/AND 运算中,求的是答案的最值。内层循环遇到 (nums[j] | x) == nums[j] 就可以提前终止了,从而达到降低内层时间复杂度的效果。而本题中要求统计子数组运算后与给定 k 相等的个数,如果 (nums[j] | x) == nums[j] 就跳出内层循环,当 k==nums[j],答案 ans 就不能得到正确累计从而出现遗漏状况。
一个解决方法是另外维护一个 List,存储子数组运算结果以及该结果对应的数量。并且不时去重合并,从而达到降低时间复杂度的效果。
数组原地去重请复习此题:🟩 26. 删除有序数组中的重复项 - 力扣(LeetCode)
1 | class Solution { |
内部循环中,ls 大小保持在 ,。
复杂度分析:
- 时间复杂度:,其中
n是nums的长度,。 - 空间复杂度:。
这个方法改写自 @灵茶山艾府 的模板方法,为了方便理解,我把原地去重的逻辑抽离出来。你可以试图将同级的两个内部循环合在一起写,就得到灵神的模板。
二分查找方法
注意到,每次外层迭代后,集合 nums[j] 值是非递减的。这时我们可以考虑 站内文章二分查找。
1 | public long countSubarrays(int[] nums, int k) { |
复杂度分析:
- 时间复杂度:,其中 n 是
nums的长度,。由于二进制数对应集合的大小不会超过 29,因此在 AND 运算下,每个数字至多可以减小 29 次。总体上看(除去二分),二重循环的总循环次数等于每个数字可以减小的次数之和,即 。 - 空间复杂度:。
个数维护方法
1 | class Solution { |
代码中,cnt 表示当层 i 中符合要求的答案数量。
复杂度分析:
- 时间复杂度:,其中
n是nums的长度,。 - 空间复杂度:。
GCD 最大公约数的计数问题
Given a sequence of integers and q queries on it. For each query you have to count the number of pairs (l, r) such that and .
is a greatest common divisor of , that is equal to a largest positive integer that divides all .
Input
The first line of the input contains integer , denoting the length of the sequence. The next line contains n space separated integers .
The third line of the input contains integer , denoting the number of queries. Then follows q lines, each contain an integer .
Output
For each query print the result in a separate line.

此题中,GCD 的运算性质和与运算类似。
此题与前面题目不同的是,它会有 q 组询问;而前面题目只有 1 组询问,这时就需要 Map 来存储不同询问的答案。
以下是输入输出代码结构:
1 | import java.util.Scanner; |
我们所需要做的是填充 solution 这个核心代码。
个数维护方法
此题是上面提到的 🟥 3209. 子数组按位与值为 K 的数目 - 力扣(LeetCode) 个数维护方法 Map 版。
1 | public static void solution(int[] nums,Map<Integer,Long> map){ |
List + 原地去重法
这里只给出 solution 方法的实现,将此函数替换上一节代码中相应函数即可。
1 | public static void solution(int[] nums,Map<Integer,Long> map){ |
相关题目:
后续计划
- 补充 CF1632D、蓝桥杯真题相关题解