和随机数生成相关的题目

语言内置的随机函数

Java 随机数获取方法：

// 随机数
Random rand = new Random(); // java.util.Random
rand.nextInt(num); // int [0,num) 
Math.random(); // double [0.0,1.0)

更多 Java 基础数学函数参见：站内文章【索引】Java 代码刷题热身。

时空权衡

🟨 382. 链表随机节点 - 力扣（LeetCode）

给你一个单链表，随机选择链表的一个节点，并返回相应的节点值。每个节点被选中的概率一样。

在这个题目的场景中，链表是已知的，相当于在一个静态数据中随机选择链表结点。我们直接想到就是把链表中的元素都放到可以随机访问的数据结构中，如 ArrayList，再通过随机数的生成进行随机选择。

// 空间换时间
class Solution {
    List<Integer> list;
    Random random;

    public Solution(ListNode head) {
        list = new ArrayList<Integer>();
        while (head != null) {
            list.add(head.val);
            head = head.next;
        }
        random = new Random();
    }

    public int getRandom() {
        return list.get(random.nextInt(list.size()));
    }
}

复杂度分析：

• 时间复杂度：初始化为 $O(n)$，随机选择为 $O(1)$，其中 n 是链表的元素个数。
• 空间复杂度：$O(n)$。我们需要 $O(n)$ 的空间存储链表中的所有元素。

我们可不可以将空间复杂度降到 $O(1)$ 呢？我们可以使用蓄水池采样算法。咱们先看代码：

// 蓄水池算法：时间换空间
class Solution {
    ListNode head;
    Random random;

    public Solution(ListNode head) {
        this.head = head;
        random = new Random();
    }

    public int getRandom() {
        int i = 1, ans = 0;
        for (ListNode node = head; node != null; node = node.next) {
            if (random.nextInt(i) == 0) { // 1/i 的概率选中（替换为答案）
                ans = node.val;
            }
            ++i;
        }
        return ans;
    }
}

对于每次选取，我们都需要遍历所有的元素。假设最终被选中的是第 k 个元素 $e_k$，这就意味着：

• 第 k 个元素 $e_k$ 前面的选取情况我们不必关心。概率为 1。
• 第 k 次选取时，需选中此元素。概率为 $P(\text{选中}e_k)$。
• 第 k+1 次选取都必须不被选中。概率为 $P(\text{不选中}e_{k+1}) \times P(\text{不选中}e_{k+2}) \times \dots \times P(\text{不选中}e_{n})$

因此，对于某个序号为 k 的元素，假设其被选中，则概率为：

$$\begin{aligned} &P(\text{函数返回}e_{k})\\ = & 1\times P(\text{选中}e_{k}) \times P(\text{不选中}e_{k+1}) \times P(\text{不选中}e_{k+2}) \times \dots \times P(\text{不选中}e_{n}) \\ = & 1\times \frac{1}{k} \times \frac{k}{k+1} \times \frac{k+1}{k+2} \times \dots \times \frac{n-1}{n} \\ = & \frac{1}{n} \end{aligned}$$

所以列表中的每个元素，均会以 $\frac{1}{n}$ 的概率被选取。

其实如果静态数据场景，要求不使用额外空间的话，可以试试随机选一个数代表链表第 n 个结点，在遍历 n 次。复杂度跟蓄水池算法差不多。

// 请勿模仿
class Solution {
    ListNode head;
    Random random;
    int n = 0;

    public Solution(ListNode head) {
        this.head = head;
        random = new Random();
        ListNode work = head;
        while(work!=null){
            n++;
            work = work.next;
        }
    }

    public int getRandom() {
        int r = random.nextInt(n);
        ListNode work = head;
        for(int i=0;i<r;i++){
            work=work.next;
        }
        return work.val;
    }
}

相关题目：

• 🟨 398. 随机数索引 - 力扣（LeetCode）。使用蓄水池采样算法会导致时间超时。

蓄水池采样算法 Reservoir Sampling

在上一小节的题目中，我们通过时间和空间的权衡，写了两种解决思路。实际上对于静态数据，每次获取随机数的时间复杂度为 $O(n)$ 的话效率实在有点低。就比如在 398. 随机数索引 - 力扣（LeetCode） 就不能使用蓄水池算法。

蓄水池采样更适合动态数据场景，如：

随机选择未知长度数据流中的某个数据

给出一个数据流，这个数据流的长度很大或者未知。并且对该数据流中数据只能访问一次。请写出一个随机选择算法，使得数据流中所有数据被选中的概率相等。

例如：

• 从 100000 份调查报告中抽取 1000 份进行统计。
• 从一本很厚的电话簿中抽取 1000 人进行姓氏统计。
• 从 Google 搜索「Ken Thompson」，从中抽取 100 个结果查看哪些是今年的。

算法的过程：

• 假设数据序列的规模为 n（对于动态数据，运行到哪，哪里就是 n），需要采样的数量的为 k。
• 首先构建一个可容纳 k 个元素的数组，将序列的前 k 个元素放入数组中。
• 然后从第 k+1 个元素开始，以 $\frac{k}{n}$ 的概率来决定该元素是否被替换到数组中（数组中的元素被替换的概率是相同的）。 当遍历完所有元素之后，数组中剩下的元素即为所需采取的样本。

一个简单的证明（当采样的数量为 1 时）已经在上一节中阐述了。下面说明当采样数量为 k 时的证明方式：

• 对于第 $i$ 个数（$i \leq k$）。
  • 在 $k$ 步之前，被选中的概率为 1。
  • 当走到第 $k+1$ 步时，被 $k+1$ 个元素替换的概率=$k+1$ 个元素被选中的概率 $\times$ 被选中替换的概率，即为 $\frac{k}{k+1} \times \frac{1}{k} = \frac{1}{k+1}$。则被保留的概率为 $1 - \frac{1}{k+1} = \frac{k}{k+1}$。
  • 依次类推，不被 $k+2$ 个元素替换的概率为 $1 - \frac{k}{k+2} \times \frac{1}{k} = \frac{k+1}{k+2}$。
  • 则运行到第 $n$ 步时，被保留的概率=被选中的概率 $\times$ 不被替换的概率，即：

$$1 \times \frac{k}{k+1} \times \frac{k+1}{k+2} \times \frac{k+2}{k+3} \times \dots \times \frac{n-1}{n} = \frac{k}{n}$$

• 对于第 $j$ 个数（$j > k$）。
  • 在第 $j$ 步被选中的概率为 $\frac{k}{j}$。不被 $j+1$ 个元素替换的概率为 $1 - \frac{k}{j+1} \times \frac{1}{k} = \frac{j}{j+1}$。
  • 则运行到第 $n$ 步时，被保留的概率=被选中的概率 $\times$ 不被替换的概率，即：

$$\frac{k}{j} \times \frac{j}{j+1} \times \frac{j+1}{j+2} \times \frac{j+2}{j+3} \times \dots \times \frac{n-1}{n} = \frac{k}{n}$$

所以对于其中每个元素，被保留的概率都为 $\frac{k}{n}$。

按权重随机选择

🟨 528. 按权重随机选择 - 力扣（LeetCode）

给你一个 下标从 0 开始 的正整数数组 w ，其中 w[i] 代表第 i 个下标的权重。

请你实现一个函数 pickIndex ，它可以 随机地 从范围 [0, w.length - 1] 内（含 0 和 w.length - 1）选出并返回一个下标。选取下标 i 的 概率 为 w[i] / sum(w) 。

对于这道题目，使用「时空权衡」小节中的方法并不能通过测试用例，要么 TLE 要么 MLE。

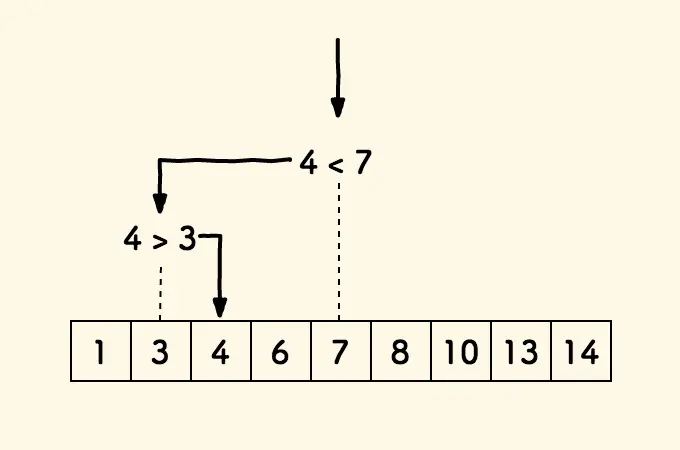
思路为使用 站内文章前缀和 + 站内文章二分查找 改进：

• 前缀和方式保证了开辟的空间不会过大；
• 生成随机数后，查找具体位置时使用二分查找可以加速效率。

class Solution {
    int[] pre;
    int[] w;
    Random rand = new Random();
    public Solution(int[] w) {
        this.w = w;
        pre = new int[w.length+1];
        for(int i=1;i<=w.length;i++){
            pre[i] = pre[i-1]+w[i-1];
        }
    }
    
    public int pickIndex() {
        int r = rand.nextInt(pre[pre.length-1]);
        int target = search(r);
        return target;
    }

    public int search(int k){
        int l = 0, r = pre.length-1;
        int mid;
        while(l<=r){
            mid = (r-l)/2+l;
            if(k>=pre[mid]){
                l=mid+1;
            }else{
                r=mid-1;
            }
        }
        return r;
    }
}

带黑名单的随机数

🟥 710. 黑名单中的随机数 - 力扣（LeetCode）

给定一个整数 n 和一个 无重复 黑名单整数数组 blacklist 。设计一种算法，从 [0, n - 1] 范围内的任意整数中选取一个 未加入 黑名单 blacklist 的整数。任何在上述范围内且不在黑名单 blacklist 中的整数都应该有 同等的可能性 被返回。

优化你的算法，使它最小化调用语言内置随机函数的次数。

通过映射，把可以进行随机的区间进行集中。

先思考一个简单的情形。假设黑名单长度为 m，且 $[0,n-m)$ 里都是白名单中的数，$[n-m,n)$ 中的数都处在黑名单。那么我们的算法就是从 $[0,n-m)$ 中随机选一个数出来就行。

在一般情况下，黑名单中的数随机分布。那么我们可以把 $[0,n-m)$ 里处于黑名单中的数，映射到 $[n-m,n)$ 中白名单的数就行，然后从 $[0,n-m)$ 中随机选一个数出来作为返回结果。

class Solution {
    Map<Integer, Integer> b2w;
    Random random;
    int bound;

    public Solution(int n, int[] blacklist) {
        b2w = new HashMap<Integer, Integer>();
        random = new Random();
        int m = blacklist.length;
        bound = n - m;
        Set<Integer> black = new HashSet<Integer>();
        for (int b : blacklist) {
            if (b >= bound) {
                black.add(b);
            }
        }

        int w = bound;
        for (int b : blacklist) {
            if (b < bound) {
                while (black.contains(w)) {
                    ++w;
                }
                b2w.put(b, w);
                ++w;
            }
        }
    }

    public int pick() {
        int x = random.nextInt(bound);
        return b2w.getOrDefault(x, x);
    }
}

概率的构造

等概率产生 0 和 1

有一个随机数发生器 f()，以概率 $P$ 产生 0，概率 $(1-P)$ 产生 1，请问能否利用这个随机数发生器，构造出新的发生器 g()，以 $1/2$ 的概率产生 0 和 1 。

不能用已有的随机生成库函数。

思路：我们可以通过随机数发生器 f()，制造一些等概率事件，并定义这些事件所表示的含义。

步骤：

• 调用两次 f()，得到以下事件的概率：
  • $P(0,0) = P\times P$
  • $P(0,1) = P\times (1-P)$
  • $P(1,0) = (1-P) \times P$
  • $P(1,1) = (1-P) \times (1-P)$
• 我们发现 $P(0,1)=P(1,0)$，那么我们可以：
  • 在 $P(0,1)$ 事件发生时输出 0；
  • 在 $P(1,0)$ 事件发生时输出 1
  • 其他时候舍弃，并重新执行步骤。（拒绝采样）
• 这样就得到了 0 和 1 均等生成的随机器了。

public int g()
{
	int i1 = f();
	int i2 = f();
	if(i1==0 && i2==1)return 1;
	if(i1==1 && i2==0)return 0;
	return g();
}

等概率产生 1 到 N 之间的数

有一个随机数发生器 f()，以概率 $P$ 产生 0，概率 $(1-P)$ 产生 1，请问能否利用这个随机数发生器，构造出新的发生器 h()，等概率产生 1~N 。

在上一部分中，我们构造了新的发生器 g() 以 $1/2$ 的概率产生 0 和 1 。假设 N 的二进制表示的位数为 k，那么我们可以调用 k 次 g()，每次 g() 生成的的结果组合成一个新的数。生成数的范围为 $[0,2^k)$，每个数被生成的几率相等。注意到，题目要求的 1~N 必然会在这个范围当中。如果生成的数符合输出要求则直接返回，否则重新生成。

🟨 470. 用 Rand7() 实现 Rand10() - 力扣（LeetCode）

给定方法 rand7 可生成 $[1,7]$ 范围内的均匀随机整数，试写一个方法 rand10 生成 $[1,10]$ 范围内的均匀随机整数。

按照之前的经验，我们需要根据 rand7 生成一些等概率的事件，并选取 10 个等概率事件对应于 1~10 数字的生成即可。对于未被选取的事件，我们将重新执行步骤。

假设 x 是这个 $[1,10n]$ 区间上的一个随机整数，那么 x%10+1 就是均匀分布在 $[1,10]$ 区间上的整数。由于 (rand7()-1)*7+rand7() 可以构造出均匀分布在 $[1,49]$ 的随机数，我们可以将 $[41,49]$ 这样的随机数剔除掉，得到的数 $[1,40]$ 仍然是均匀分布在 $[1,40]$ 的。

证明 (rand7()-1)*7+rand7() 可以构造出均匀分布在 $[1,49]$ 的随机数

(rand7()-1)*7 得到一个离散整数集合 $A=\{0，7，14，21，28，35，42\}$，其中每个整数的出现概率也都是 $1/7$。

rand7() 得到的集合 $B=\{1,2,3,4,5,6,7\}$ 中每个整数出现的概率也是 $1/7$。

显然集合 A 和 B 中任何两个元素组合可以与 $[1,49]$ 之间的一个整数一一对应，也就是说 $[1,49]$ 之间的任何一个数，可以唯一确定 A 和 B 中两个元素的一种组合方式，反过来也成立。

由于 A 和 B 中元素可以看成是独立事件，根据独立事件的概率公式 $P(AB)=P(A)P(B)$，得到每个组合的概率是 $1/7\times 1/7=1/49$。因此 (rand7()-1)*7+rand7() 生成的整数均匀分布在 $[1,49]$ 之间，每个数的概率都是 $1/49$。

class Solution extends SolBase {
    public int rand10() {
        int row, col, idx;
        do {
            row = rand7();
            col = rand7();
            idx = col + (row - 1) * 7;
        } while (idx > 40);
        return 1 + (idx - 1) % 10;
    }
}

复杂度分析：

• 时间复杂度：期望时间复杂度为 $O(1)$，但最坏情况下会达到 $O(∞)$（一直被拒绝）。
• 空间复杂度：$O(1)$。

下面是对 rand7() 函数调用次数期望的探讨。在上面的方法中，假设连续调用两次 rand7() 为一轮，那么有：

• 第一轮中，有 $\frac{40}{49}$ 的概率被接受，$\frac{9}{49}$ 的概率被拒绝
• 第二轮中，有 $(\frac{40}{49})^2$ 的概率被接受，$(\frac{9}{49})^2$ 的概率被拒绝
• 第 n 轮中，有 $(\frac{40}{49})^n$ 的概率被接受，$(\frac{9}{49})^n$ 的概率被拒绝

$$\begin{aligned} E(\#\text{calls}) &= 2 + 2 \cdot \frac{9}{49} + 2 \cdot \left(\frac{9}{49}\right)^2 + \dots \\ &= 2 \sum_{n=0}^{\infty} \left(\frac{9}{49}\right)^n \\ &= 2 \cdot \frac{1}{1 - \frac{9}{49}} \\ &= 2.45 \end{aligned}$$

我们可以通过减少被拒绝的概率，从而减少函数调用的期望。我们可以通过合理地使用被拒绝的采样，从而对方法一进行优化：

• 在上面的方法中，我们生成 $[1,49]$ 的随机数，若生成的随机数 x 在 $[41,49]$ 中，我们则拒绝 x。
• 然而在 x 被拒绝的情况下，我们得到了一个 $[1,9]$ 的随机数，如果再调用一次 rand7()，那么就可以生成 $[1,63]$ 的随机数。我们保留 $[1,60]$ 并拒绝 $[61,63]$。
• 如果还被拒绝，我们还是得到了 $[1,3]$ 的随机数。我们继续调用 rand7()，生成 $[1,21]$ 的随机数，保留 $[1,20]$ 并拒绝 $[1]$。
• 此时 $[1]$ 已经没有任何用处，若出现了拒绝 1 的情况，我们就重新开始生成 $[1,49]$ 的随机数。

假设经过上面的优化步骤为一大轮，每轮有 3 次尝试，那么有：

• 第一次尝试，有 $\frac{40}{49}$ 的概率被接受，$\frac{9}{49}$ 的概率被拒绝
• 第二次尝试，有 $\frac{60}{63}$ 的概率被接受，$\frac{3}{63}$ 的概率被拒绝
• 第三次尝试，有 $\frac{20}{21}$ 的概率被接受，$\frac{1}{21}$ 的概率被拒绝

$$\begin{aligned} E(\#\text{calls}) &= 2 + 1 \cdot \frac{9}{49} + 1 \cdot \frac{9}{49} \cdot \frac{3}{63} + 2 \cdot \frac{9}{49} \cdot \frac{3}{63} \cdot \frac{1}{21} + \dots \\ &= \left( 2 + \frac{9}{49} + \frac{9}{49} \cdot \frac{3}{63} \right) \cdot \frac{1}{1 - \frac{9}{49} \cdot \frac{3}{63} \cdot \frac{1}{21}} \\ &\approx 2.19333 \end{aligned}$$

本文参考

• 蓄水池采样算法（Reservoir Sampling）原理，证明和代码-CSDN博客
• 蓄水池采样算法（Reservoir Sampling） - alfred_zhong - 博客园
• 概率p输出1，概率1-p输出0，等概率输出0和1 & 【LeetCode】470. rand7()构造rand10() 系列变形（新浪、字节面试题）_有一个函数f(),以p概率生成,1-p概率生成1,现在需要调用这个函数,以0.5概率生成0和-CSDN博客
• 使用随机函数生成等概率分布-CSDN博客