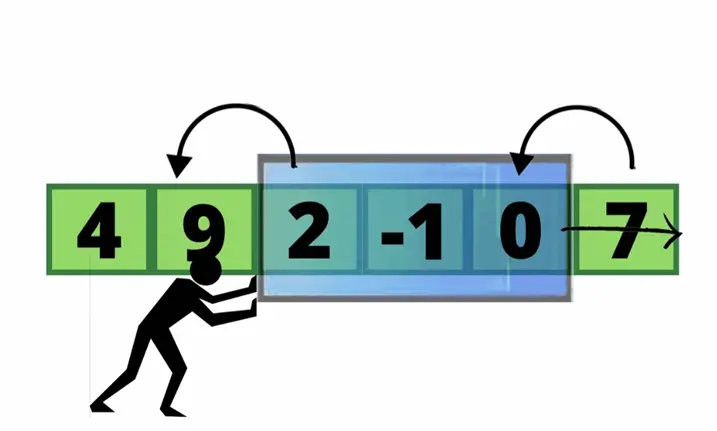
差分数组
摘要生成中...
AI 摘要
Hunyuan-lite
差分数组是前缀和的逆运算。
本文题目难度标识:🟩简单,🟨中等,🟥困难。
一维差分
对于数组 a,定义其差分数组(difference array)为
差分数组具有以下性质:
- 性质 1:从左到右累加 d 中的元素,可以得到数组 a。
- 性质 2:如下两个操作是等价的。
- 把 a 的子数组 都加上 。
- 把 增加 ,把 减少 。
观察性质 2,原本 的操作可以变为 的操作,然后通过性质 1 使用 的时间恢复数组 a。性质 2 也告诉我们差分数组是怎么影响原数组的。当 发生变动,如加 1,表示把 a 中下标 i 及后面的数都加上了 1。
本节例题 🟨 1094. 拼车 - 力扣(LeetCode)
1 | int[] diff = new int[1003]; |
相关题目:🟩 2848. 与车相交的点 - 力扣(LeetCode)
如果差分数组的数据比较稀疏,或构建差分数组的长度过大,那么在实现差分数组时除了建立一个 Array 数组外,还可以使用 Map 替代数组记录下标和值的键值对。
Java 具体做法为,使用 TreeMap 或使用普通 Map,再对 key 做一次排序。
1 | Map<Integer,Integer> map = new TreeMap<>(); |
相关题目:
二维差分
从一位差分数组到二维差分数组:

原数组的还原方式:计算二维前缀和即可还原。
相关题目:
本文参考
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 半方池水半方田!
评论