本文题目难度标识:🟩简单,🟨中等,🟥困难。
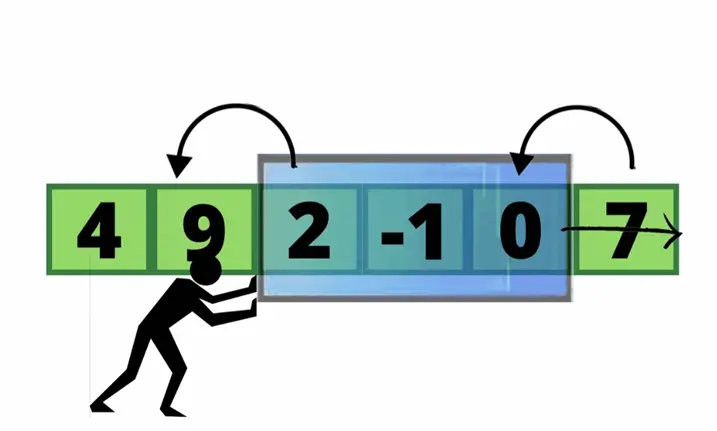
直观感受树状数组
树状数组是一种支持「单点修改」和「区间查询」的,代码量小的数据结构:
- 单点修改:给定数组
arr,将 arr[i] 自增为 k。这里的自增可以是赋值等其他操作。 - 区间查询:给定
l、r,求 arr[l..r] 的和或其他区间特征。
普通树状数组维护的信息及运算要满足 结合律 且 可差分,如加法(和)、乘法(积)、异或等。
- 结合律:(x∘y)∘z=x∘(y∘z)
- 可差分:具有逆运算的运算,即已知 x∘y 和 x,可求出 y。
事实上,树状数组能解决的问题是 站内文章线段树 能解决的问题的子集:树状数组能做的,线段树一定能做;线段树能做的,树状数组不一定可以。然而,树状数组的代码要远比线段树短,时间效率常数也更小,因此仍有学习价值。
通过对树状数组进行扩展,我们还可以使其进行「区间修改」和「单点查询」:
- 区间修改:给定
l、r、k,将 arr[l..r] 中的每个数自增 k。这里的自增可以是其他操作。 - 单点查询:给定
x,求 arr[x]。
比如,在差分数组和辅助数组的帮助下,树状数组还可解决「区间加求单点值」「区间加区间和」问题。
树状数组的构建逻辑

树状数组中的结点 c[i] 管辖了原数组 a 中的一个范围,a[l..r],l≤r。比如:
c[i] 的值为 a[l..r] 的和;a[i] 会直接交给 c[i] 管辖;- 树状数组的
index 是 1-base 的,c[0] 不管辖任何内容。
树状数组只有一个父结点,c[i] 的父结点为 c[i+lowbit(i)]。这是它构建树的核心原理。反过来推断,c[i] 子节点的序号 z 将满足 z+lowbit(z)==x。
函数 lowbit(x) 表示 x 二进制表示中,最低比特位所代表的数。比如:
lowbit(0b1101010)=0b10lowbit(0b0101000)=0b1000
它的实现为 (x)->x&-x,具体原理可以看这篇文章:站内文章位运算技巧总结。
c[y] 是 c[x] 的祖父结点,意味着 x 能通过不断加上 lowbit 能得到 y。

具体的性质与证明详见:树状数组 - OI Wiki。
树状数组基本操作
本节将以树状数组维护区间和为例。
单点修改区间查询模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public class Main{
public static int[] arr;
public static void main(String[] args) throws IOException{
int n = nextInt();
arr = new int[n+1];
int[] nums = new int[]{1,2,3,4,5,6,7};
buildTree(nums);
}
public static void add(int index,int val){
int cur = index;
while(cur<arr.length){
arr[cur]+=val;
cur+=lowbit(cur);
}
}
public static int sumRange(int x,int y){
int l = sumR(x-1);
int r = sumR(y);
return r-l;
}
public static int sumRange(int x){
int cur = x;
int ans = 0;
while(cur>0){
ans+=arr[cur];
cur-=lowbit(cur);
}
return ans;
}
public static int lowbit(int x){
return -x&x;
}
}
|
复杂度分析:
- 时间复杂度:
- 单点修改:Θ(logn)。
- 区间查询:Θ(logn)。
- 空间复杂度:O(n)
建树
最基本的建树方式就是对于原数组中的每个 nums[i],都执行一遍 add 操作。时间复杂度 O(nlogn)。
1
2
3
4
5
6
| public void static build(int[] nums){
for(int i=0;i<nums.length;i++){
int cur = i+1;
add(cur,nums[i]);
}
}
|
我们还可以使用更快的 O(n) 建树技巧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public void static build(int[] nums){
for(int i=0;i<nums.length;i++){
int cur = i+1;
arr[cur] += nums[i];
int p = cur + lowbit(cur);
if(p<=n) arr[p] += arr[cur];
}
}
public void static build(int[] nums){
for(int i=0;i<nums.length;i++){
int cur = i+1;
arr[cur] = sum[cur] - sum[cur-lowbit(cur)];
}
}
|
树状数组变形
区间加求单点值或区间和
「区间加求单点值或区间和」与基本树状数组不同的是,要求树状数组实现区间修改。
对于基本树状数组,每次进行单点修改很容易。如果题目进行区间修改,一个想法是对区间范围不断进行单点修改,这样的效率会很低。站内文章差分数组 可以解决这个问题。
考虑查询 a[1..r] 的和:
i=1∑raii=1∑rj=1∑idj=i=1∑rj=1∑idj=i=1∑rdi×(r−i+1)=i=1∑rdi×(r+1)−i=1∑rdi×i
观察式子可知,我们可以用两个树状数组维护 d[i] 和 d[i]*i 的信息。
「求单点值」的问题比「求区间和」更弱。下面代码给出了「区间加区间和」所需要的数据结构与方法,main 函数中依照题目要求,只使用了「求单点值」的做法。稍作改动就可实现「求区间和」。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| import java.io.*;
public class Main {
public static long[] sumD;
public static long[] sumDi;
public static void main(String[] args) throws IOException {
int n = nextInt();
int m = nextInt();
sumD = new long[n + 1];
sumDi = new long[n + 1];
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
int e = nextInt();
arr[i] = e;
}
int[] d = new int[n];
d[0] = arr[0];
for (int i = 1; i < n; i++) {
d[i] = arr[i] - arr[i - 1];
}
build(d);
for (int i = 0; i < m; i++) {
int op = nextInt();
if (op == 1) {
int x = nextInt();
int y = nextInt();
int k = nextInt();
add(x, y, k);
} else {
int x = nextInt();
System.out.println(sumR(x, x));
}
}
os.flush();
}
public static void add(int x, int y, int val) {
add(x, val);
add(y + 1, -val);
}
public static void add(int x, int val) {
int cur = x;
while (cur < sumD.length) {
sumD[cur] += val;
sumDi[cur] += (long) val * x;
cur += lowbit(cur);
}
}
public static long sumR(int x, int y) {
long xx = (long) (x) * sumR(sumD, x - 1) - sumR(sumDi, x - 1);
long yy = (long) (y + 1) * sumR(sumD, y) - sumR(sumDi, y);
return yy - xx;
}
public static long sumR(long[] a, int x) {
int cur = x;
long sum = 0;
while (cur > 0) {
sum += a[cur];
cur -= lowbit(cur);
}
return sum;
}
public static int lowbit(int x) {
return -x & x;
}
public static void build(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int cur = i + 1;
sumD[cur] += arr[i];
sumDi[cur] += (long) arr[i] * cur;
int newCur = cur + lowbit(cur);
if (newCur < sumD.length) {
sumD[newCur] += sumD[cur];
sumDi[newCur] += sumDi[cur];
}
}
}
static StreamTokenizer sc = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter os = new PrintWriter(System.out);
static int nextInt() throws IOException {
sc.nextToken();
return (int) sc.nval;
}
}
|
本文参考